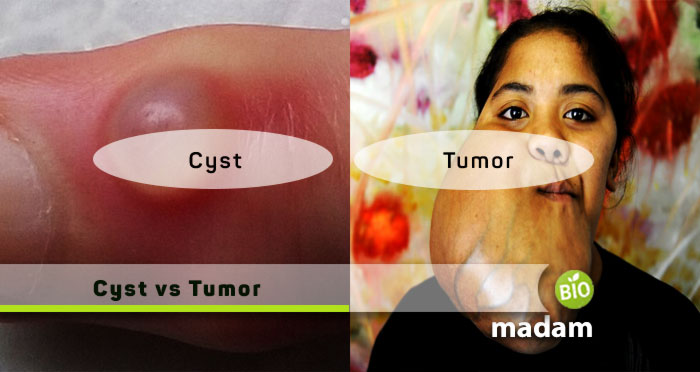
Biomadam’s core belief in life sciences revolves around providing its complete information. This website is particularly designed to comfort students, so they can easily grab the concepts confusing them. We are well aware that every student studies and learns differently, so we collaborated with a team of highly skilled people.
Follow us on your Favorite Social Media

For many women, the first few months of pregnancy can mean dealing with the…
Water birth consists of giving birth in a tub of warm water, typically at…
Pregnancy is a time of happiness, but it brings changes and sometimes aches. One…
Embarking on the journey of understanding how long a miscarriage takes once bleeding starts…
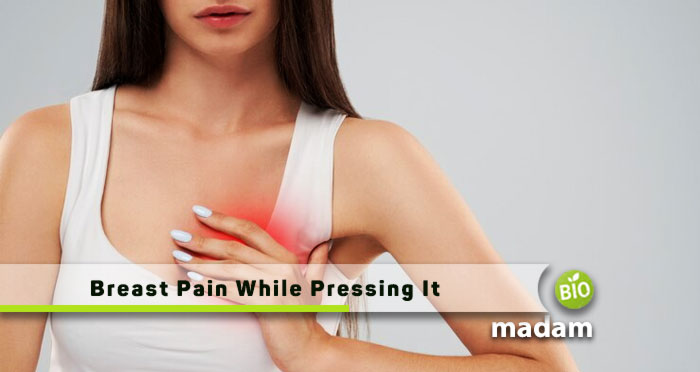
Breast pain, or mastalgia, is a common concern that prompts many individuals to seek…
Embarking on the path to parenthood is a joyous journey, but it’s essential to…
Family Interactions Help Prevent Crime in Society.

Are you tired of the confusing world of lingerie and the myriad of options…
Embarking on the journey to find the perfect-fitting bra is a pursuit of comfort,…
For thousands upon thousands of years, the deserts of Australia have been home to…
How Far is Savannah From Atlanta
Things to do in Aguadilla Puerto Rico
30th Birthday Trip Ideas for Her
How Far is Houston from Dallas
How Far is San Juan from Aguadilla?
How Far is Fort Myers from Miami?
9 Cheapest Countries To Visit In Europe in 2024
Is it Safe to Travel to Turkey as a Woman?
-
Are There Travel-Friendly Breastfeeding Chairs Available?
Embarking on a journey of motherhood is a voyage unlike… Full Article
-
What Safety Features Should I Look for in a Breastfeeding Chair?
Welcome to the world of breastfeeding, where every moment between… Full Article
-
Why are Nursing Chairs so Low?
When it comes to caring for a newborn, comfort and… Full Article
-
Can I Use a Breastfeeding Chair for Bottle Feeding too?
When it comes to feeding your baby, comfort and bonding… Full Article